Rake's Progress

RAKE'S PROGRESS

Steering Geometry: Why the Numbers Can’t Tell You What Everybody Knows

Lane Campbell

It seems so simple. You can look at a schematic of a motorcycle's front end and quickly pick apart the elements of steering geometry: rake and trail. It's fairly common knowledge. Rake is synonymous with steering head angle. usually measured in degrees from vertical. Trail is the distance between the actual contact patch and that imaginary point where the steering head axis strikes the ground.

You look at the diagram, sitting there so innocently on a piece of paper, and it all appears cut and dried. Everybody knows (?) that if you increase head angle you increase high-speed stability at the expense of quickness; and that if you decrease head angle you speed up the handling at the expense of stability. Everybody knows (?) that trail is something you’ve got to have in order to keep the contact patch from momentarily leading the steering axis. (If that happens, the steering suddenly wants to swap ends, as many a trials rider has found out the hard way. )

But why? Why do certain combinations of rake and trail work better than others? Why do short-trackers work with 24-26 deg. of head angle, road bikes with 27-30 deg. and motocrossers with 29-31 deg? Nobody knows—or if they know, they aren’t talking.

The trouble with understanding steering geometry in motorcycles is that while the bike is capable of flopping about in threedimensional space, our thinking is geared to w hat we can draw on a two-dimensional piece of paper. Because magazines are (as yet) printed on two-dimensional paper, we have a bit of a problem getting the idea across.

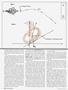
Start with the conventional way we look at steering geometry, the good of side elevation view (See Fig. 1). If you're a motorcycle designer starting with a clean sheet of paper, the first thing you draw is a front wheel and the ground. You drop a line straight down from the axle center, and there's your contact point on level ground.

You want trail? Pick a number. Say 5 in. OK, scale off 5 in. ahead of the contact patch and call that point “P”. Pick another number for rake. You like 30 deg.? OK. from point “P”. draw a line angled back 30 deg. from vertical. You’ve just taken the first step toward locating your steering head. That line is your steering axis, and your steering head has got to be somewhere on it—preferably far enough away from the wheel to allow for suspension travel, but not so far as to make the motorcycle excessively top-heavy.

And that’s how the design of every motorcycle front end begins. Honest. Sure, you're not used to thinking about it that way. because you. most likely, are sitting in your garage, looking at a motorcycle that's already built, and thinking, “Now if I change this, what will happen to that?" You're correct—any simple modification made to your front end w ill usually change rake and trail simultaneously, and not always the way you wanted.

But in the beginning, rake and trail started as numbers in the designer’s head. Bv picking them, he begins to determine the size and shape of all the front end components—the fork legs, sliders, triple clamps, the front third of the frame, even (to some extent) the size and routing of the exhaust pipe(s).

Uh. I’ve left out something rather crucial haven't I? How’d he pick the numbers, in the first place? Is he using some secret formula nobody else knows? Or is he using rule-of-thumb, based on what works—as “everybody knows?’’ I hate to burst anybody's bubble, but historically, most builders have picked the numbers by trial and error first; the understanding of “why” has come after they saw what worked and what didn’t.

So how do these quantities—rake and trail—work for you (or against you)? Viewing the motorcycle two-dimensionally, and in the straight-up mode, you could say, as with a car, trail gives you self-centering action and rake (or head angle) helps the steering flop in the desired direction.

Hmm. If you begin to question and test these assumptions, the two-dimensional, straight-up, non-dynamic analysis begins to strain at the seams. For instance: Selfcentering action due to trail (or caster, as the car folks call it) is a stabilizing force. Yet steering flop, due to rake, is a destabilizing force.

Does this suggest that steering geometry is a precarious balance between basically opposite types of forces? The balance of a well-designed motorcycle doesn’t seem all that precarious ... in fact, it will take considerable abuse to unbalance the better examples of the builder's art. There must be more to it.

OK. let’s look at trail, by itself, still straight up, and let’s get dynamic about it. Write rake out of the picture, assume a vertical steering axis (see Fig. 2, side view) and let the steering axis lead the contact patch by some set amount.

Now, with the motorcycle rolling forward so there’s some drag on the contact patch, let's disturb the steering away from straight-ahead. That drag on the contact patch immediately creates a self-centering torque (or moment) about the steering axis. (View the system vertically, as in Fig.

2. top view, and see how this is so; don't just depend on your intuition.)

Although you may get self-centering force immediately, things don’t happen immediately. The reason is inertia. Yep, New ton’s first and second laws are at work.

It takes force to get something moving, and once moving it takes force to get it stopped.

It works for things that go in straight lines, like accelerating or decelerating motorcycles. It also works for things that rotate. Fike wheels, like the steering mechanism (forks, wheel and all) as it rotates about the steering axis, even like the whole motorcycle as it rotates about its roll axis when you lean it. Keep these ideas of rotational inertia in mind. You’ll need them.

Back to our castered steering. It’s out of line, it's got a self-centering force acting on it, it starts to move. It moves back toward straight-ahead, and because the package does have inertia, it keeps on moving right past straight-ahead. Once it does that, it’s subject to a self-centering force in the opposite direction. That slows the motion, ultimately reverses it. and sets it off in the other direction. In slow motion, I’ve just described steering shimmy, as is exhibited by worn out shopping carts and some worn out (or poorly set up) motorcycles.

So trail (or caster) alone is not enough. You already knew that by rule of thumb. Let’s put the rake back in. Standing still, the steering is now somewhat like a broomstick balanced on end. As long as it's perfectly vertical, the weight (acting through the c.g.) is right in line with the support. Let it get one smidgin off vertical, and those forces are no longer in line. Over she goes.

Take any bike, sitting on the floor. Put a little weight on it. lean it a bit. and the steering will flop. Try pushing it with hands oft'the bars. Gotta be careful at lirst. huh? Get it the least bit imbalanced, and— FLOP! You’re at full lock, headed for the wall. But. if you get it rolling, even at a walk,you can lean it a bit and it will selfsteer. The steering will flop just enough to maintain a gentle curve, but no further.

So the self-centering force due to trail is very much there, strong enough to overshadow the flopping effect due to rake. The rake effect, evidently, is just enough to dampen the shimmying tendency of the castered front wheel. Meanw hile, the contrary effects of both are further damped bv the spinning w heel acting as a gvro. More about that later.

Well, that’s part of the picture. But there are a w hole lot of things unaccounted for. Motorcycles don't spend all their time straight up. or rolling around the shop floor. In reality a cornering motorcycle, particularly its front end, is being pushed pretty hard in several directions.

First, there is weight. Pressing doyvn on the front w heel is some fraction of the total man/machine yveight. determined by the front/rear weight distribution. Conversely, the ground is pressing up against the tire contact patch with an equal and opposite force. Newton’s third law is alive and well.

Next, there is cornering force. It acts at right angles to the motorcycle’s path. Its magnitude (i.e.. how much) depends on the amount of lateral acceleration (measured in “g's” multiplied by the total man/ machine yveight. (See “May the Force Work with You,” CW January l978.)The amount acting through the front tire contact patch, again, depends on weight distribution fore and aft.

Third, there is drag. At minimum, it is the free rolling resistance of wheel and tire. At maximum, it could be the ultimate power of a fully applied front brake, or more likely, the ultimate tractive power of the front tire. Under braking, weight distribution can change dramatically, so those two previously mentioned forces will vary under braking proportionally.

Finally, there is a torque—a tyvist or a moment about the steering axis, applied by the rider through the bars. This, too, ends up reacting through the tire contact patch. This force, by the wav. is not quite so pre-ordained as the other three. It's at the mercy of the rider, dependent on his skill and discretion (or lack of same).

With the bike cranked over at some lean angle, each of these forces, taken alone, has some influence on the steering. Weight, taken alone, would make the steering flop. Cornering force, taken alone, would act just the opposite, would straighten the steering, eyen force it into opposite lock. Drag, because of a quirk of geometry, (see Fig. 3) tends to pull the steering doyvn, or to flop it. Steering torque, taken alone, also has interesting side effects. Exerted in a direction opposite the vehicle's turn it has a “lifting” effect on the front end. Exerted in the same direction as the turn, it would tend to loyver the front end.

Once again I seem to have painted a picture of a system in precarious balance. T hat it does balance is obvious knoyvledge, dating from the first time you pitched a properly set-up motorcycle into a turn. Our two-dimensional, piece-at-a-time analysis isn't really together with reality. Yet.'

So let's finally take a crack at the system in three dimensions. Fig. 4 shows a cornering motorcycle, superimposed on three dimensional axes—the X in the direction of travel. Y at right angles along the ground, and Z vertical. F. W. and D (drawn to scale) are the reaction forces (ground against the tire) of cornering force, yveight and drag, respectively.

Now take away the motorcycle, for a moment. Fig. 5 shows how a junior draftsman (or engineering flunky) would graphically resolve these three forces into one summation, or resultant force R. In a three-dimensional model, this projection technique would give you. to scale, the true magnitude and direction of R. Because we’re trying to represent a three-dimensional model in perspective on a twodimensional piece of paper, R is going to be somewhat distorted and foreshortened in the drawing. It's hanging out there in an “imaginary” space, and you have to make that connection in your mind. Not easy.

OK. in Fig. 6. we put back the motorcycle. complete with steering axis (dotted line to P). In the drawing, R appears to cross the steering axis. I say “appears,” because in this kind of rough perspective sketch, there is no way, without much additional, complex (and believe me. painful) dimensional analysis that I can prove that it does. The two lines could be skewed: i.e., non-parallel lines that are in different planes, therefore need never meet.

However, I did not float this sketch as a nuts-on map of three-dimensional space: I actually brought up the preceding point to show that perspective sketches can be deceptive. What I will prove, however (now that we’re at least thinking and wondering in three dimensions) is that for steering stability, the two lines must meet.

Let’s just say they don’t; that they are skew. So you’ve got this resultant force R. pressing hard on the front tire contact patch, acting on an imaginary line that passes the steering axis at some distance. If that is true, the net effect of R has to be a moment (or torque, or twist) about the steering axis—a moment that the rider must resist, through the bars, or else the steering is going to move in the direction of that unresisted torque.

There are only two conditions in which there would be zero moment, hence no disturbance to the steering. One is if the line-of-action of R crosses the steering axis. The other is if the two lines are parallel (possible, but not very likely). Therefore, a motorcycle which is set up for the purpose intended (be it road racing, trials, short track, whatever) has steering geometry chosen so that, when used as intended, the commonly encountered cornering forces yield a resultant force R whose line of action passes through, or very near, the steering axis.

By now, you’re thinking, “This is just too much to swallow', all at once.” I can’t help but agree. So far. I’ve managed to skip from pinnacle to pinnacle in a subject which, properly, could take up a whole 10week course, part of a college curriculum called Motorcycle Design Engineering (a private, pet dream of mine).

In the telling. I’ve not told the whole story of the variable and dynamic forces that play about a motorcycle’s front end. I’ve taken isolated pieces of the story and pushed them until some facet of the illustration or example begins to break down under analysis. With a purpose. There’s more here than the mind can grasp with pencil-and-paper tools.

That suggests the entry of a computer into the fray; and some Japanese gentlemen, Yoshinori Watanabe and Keigo Yoshida of Honda R&D, have done some fine research in this area. This was no ivory-tower exercise. They got their base data and continued cross-checking, using instrumented motorcycles of various sizes, with several skill levels of rider aboard.

The experiment involved approaching an obstacle at different pre-determined speeds, and at the last possible moment flashing an arrow that indicates whether the rider should pass the obstacle to the right or left. (See Fig. 7.) This forces the rider to throw his weight hard on the bars, bank that mother right down to the pegs and make it turn just as quickly as he can.

In doing this work, they not only fiddled with steering geometry and other machine factors, but also got a really firm handle on the differences between skilled rider techniques and beginning rider techniques and how they affected a bike’s accident avoidance capability.

They instrumented the bikes so they could get a running graph of things like the rider’s body angle, the bike’s lean angle, the amount of torque the rider was exerting through the handlebars, the angle of the steering, the bike’s actual path. This gave them a picture of reality. Then they retired to the ivory tower and proceeded to create a computer simulation program which, once set running, would come up with the same kind of response.

To do so, they w'rote up seven separate equations of motion, relating to the motorcycle as a whole and to pieces of the motorcycle, as free bodies. These w'ere in addition to the normal equations of motion which describe the bike’s path over the ground. Stuffed into these equations were at least 51 different factors—some constant, some variable, some really hairy. They cranked it all in: weights sprung and unsprung, front/rear springing and damping rates, moments of inertia for rotation in all three directions (yaw, pitch, roll) for the whole motorcycle and pieces of it, front end geometry, triple clamp offset and more.

The important thing is, it worked. The computer model spat out graphs that were so close to the real thing, it was amazing. (With most computer programs I’ve ever played with, if the machine gave you even a rough approximation of reality half the time and spat out garbage the other half, you called it a success.)

Think about this a minute. It took an intellectual effort that would boggle the mind and fill a book in order to generate data that you can also get by just taking a motorcycle out and riding it. That’s not to say it was a wasted exercise, for it gave them a tool with which to construct meaningful data on handling for motorcycles that don’t exist yet. And that's something.

More important to you and me. by going through the motions they created ways in which you and I can visualize what happens when you throw a bike hard into a turn, starting from straight up. Fig. 8 show's a set of lines which could have been generated by computer or by actual test—take your pick. They are four of the most relevant factors in the behavior of the cornering man/motorcycle complex.

Definition time. Steering moment is the force thrown into the steering mechanism by the rider in an effort to make it turn. (Torque exerted on the handlebars.) Steering angle is how much the steering has actually turned in response to that force. Banking angle is the lean angle for the whole motorcycle; and path (relative to the original direction before the turn) is sort of self-explanatory.

Notice some rather interesting things (assuming you didn't already know them). Say the guy wants to turn right. Yet the very first thing he has done is twist the bars hard left. The steering has turned left, the bike’s path goes left, while the bike as a whole begins to smoothly bank right. Once it’s banked, then the bike as a whole begins to curve right, crossing the original path and heading in the intended direction. As this takes hold, the rider neutralizes his heavy torque on the steering, and the steering (with a couple of slow corrective wobbles) just kind of flops into a stable cornering attitude, slightly right of neutral.

Some riders already know this in their bones. If it’s not that way with you, either think back to your last ride or take your bike out and try it. Sure enough, when you really want to throw it down quick, you lean hard on that low-side bar, in effect twisting the steering in the opposite direction to your desired turn, just long enough to set up that turn.

As ever, there's more than one phenomenon at work. First, just by cranking the steering left, you kick the bottom of the bike left while the top is still overcoming its inertia. The result is a quick-breaking right bank, which will ultimately make the bike turn right.

The second thing operating is the gyroscopic action of the front wheel itself. A motorcycle wheel, with most of its weight concentrated near the rim, is one very efficient gyro. Like any other gyro, it resists being disturbed. This, in turn, makes motorcycles and bicycles quite stable when rolling.

However, a constant torque on the handlebars is the kind of disturbance that won't go aw'ay. So the gyro responds to the disturbance through a phenomenon called “precession.” The mathematics of it are hairy and all but forgotten. The upshot of it is this: When a gyro is disturbed by a forceful torque at right angles to its spinning axis, it kicks back with an equivalent torque that’s at right angles to both its spinning axis and to the original torque.

That sound like a mouthful? Let's put in context of a motorcycle front wheel. The axle is the spinning axis. The steering head is at right angles to the axle. You crank the bars left, and the spinning wheel is going to kick back with a force tending to make the whole works bank right! The axis of this “kickback” torque is at right angles to the steering head and to the axle as well.

continued on page 60

continued from page 56

Now. if there were zero rake, then the spinning axis of the wheel is parallel to the pitch axis of the bike; the steering head is parallel to the yaw axis of the bike; and the “kickback” axis from gyro precession is the roll axis of the bike. Gyro precession of the front wheel forces the bike to roll (or bank, or lean) in the direction opposite to that in which the bars are being tw isted.

Still here? OK, now visualize some rake being applied to the steering head. When the bars are twisted, the kickback from gyro precession is still at right angles to the steering head, but it no longer coincides with the roll axis of the bike. Hmm. What does that mean?

With a little bit of rake, it means that a large proportion of the precession torque is still operating to make the bike roll (say) right. At the same time, the remaining, and far smaller, proportion of precession torque is trying to make the bike yaw left.

So. As rake increases, a smaller portion of precession torque is available to force the bike to lean in the desired direction, while a larger portion is working to make the bike yaw opposite the intended direction. Net effect is a slower response to rider input from this source (which, as mentioned earlier, is only one force among many).

1 would also suggest another humanfactor's effect of rake, though I’m not in a position to prove it. When the rider leans into a turn and presses on that low-side bar. he’s pushing straight from the shoulder. making for a thrust against the bar that's angled down and forward. This, in turn, means that part of his thrust goes into useful torque about the steering head, and part of it just goes to bending the bar down. The greater the steering head rake, the more of the rider’s weight is going to be lost to downward pressure, leaving less of his weight/strength to exert useful steering torque.

This brings to mind two observed phenomena. not wholly unrelated. (1) I've watched a number of my road-racing acquaintances break off their clip-ons at the roots from leaning on them too hard, trying to force their way into a turn. (In fact, my partner and I won a race by default that way. once.) (2) The late Jarno Saarinen favored special clip-ons with such a radical droop that they became a personal trademark. The “Jarno bars,” by their radical droop, force the rider to thrust forward on them instead of down, thus giving him much more effective leverage about the steering head. (Plus, they tend to help him tuck in better.)

At any rate, the effect of increasing rake seems to be at least twofold. In both cases, the outcome is to slow or retard the motorcycle's response to rider input. (Which you expected all along, right?)

As a teaser in their report, the Japanese did a simulation comparing a stock CB750 with a 27-deg. head angle to a hypothetical CB750 with a 40-deg. head angle. At 30 mph (which is fairly slow) the increased rake delayed the bike’s response by a full half-second at full bank. I might add that the faster you go. the more important gyro effect becomes. It increases as the square of speed. Which means that at racing speeds, even variations of less than a degree in head angle are going to have an effect the rider can feel. This applies not only to permanent frame mods, but to the transient pitching of the frame on its suspension.

That’s of little consequence to stiffly sprung road racers, rigid-framed speedway bikes or fully set-up dirt trackers. Once they’re set up right, they’re set. But for softly sprung street bikes, and especially for long-travel dirt bikes, the normal travel of the working suspension can create problems.

As an example, take a motocrosser with 10 in. of travel front/rear. a head angle at rest of 30 deg., and a trail at rest of 7 in. (Fig. 9.) Cycle it through the extremes of its suspension travel (i.e.. rear compressed and front extended to front compressed and rear extended) and you get some radical things happening to your steering geometry. (Fig. 10a, 10b.) In a situation like this, there’s no way the designer can pick one set of “right” numbers for this sort of machine. The best he can strive for is a setup that can live through all the variations of which the bike is capable. Even then, to be both safe and competitive, the rider is required to adopt special techniques to avoid having the suspension come up at the wrong extreme in the wrong place.

continued on page 62

continued from page 60

Mention was made earlier of the apparent contradiction between what on paper is a set of imbalances and what we know firsthand to be a balance, that is, the motorcycle is stable and can be steered.

What all the engineering terms and methods come down to, for the purposes of this investigation, is simply that the forces do balance, and that when and how they balance depends on the rake angle and trail length.

This variation controls quickness of steering, as we’ve seen in real life and via the computer study.

The steeper the rake, which is to say the closer to vertical, the quicker the steering.

Now we're down to it. A flattrack racing bike must steer quickest of all. The rider must slam into the turn, hurl the machine into a slide and balance the bike in that slide, under power, until it’s time to wrench the thing upright and shoot off down the straight. Trackers do not go straight on the straight. What they do is proceed in a series of tank-slappers-to-be. The riders put up with it, because that's the price you pay for glorious slides and slides is how you win.

Much the same for trialers, which must turn quickly at slow speeds and need not go straight except when darting through the woods from section to section.

A road motorcycle has more rake, in terms of being further from vertical. Not much more. A road bike has good traction. The soft rubber and grainy paving can actually gear themselves together and you can have better than a 1:1 coefficient of friction. (That’s how the dragsters do better on the strip than the science textbooks say they can. The scientists based their predictions on a grip of 1:1.)

Rake angles become further from vertical off-road. The main reason is that the dirt bike must have slow' steering because it doesn’t have grip. Like brakes. You don't want powerful brakes on an enduro bike because you'll lock the wheels.

Off-road geometry has its own sliding scale. Motoerossers need to turn quickly and they usually have traction (or a berm) and they don’t have much top speed, so most motocross machines are steeply raked.

An enduro bike works best with slower steering while still needing quickness for the tight places.

A pure desert racer (or the cowtrailer’s sled) has to be able to go straight. Sharp turns can be slowed down for or slid through, so the Husqvarnas and Hondas out in the w ide open spaces run perhaps 3 1 or 32 deg. rake.

Beyond that, all those little rocks and ruts and gullies are constantly banging the front wheel this way and that. The more rake and trail, the more centering action to keep the bike straight. An otf-road racer needs all the straightness he can get.

Finally, the dirt machine has to begin with more trail than it needs. We have the of steering axis out front, right? And the contact patch is directly beneath the axle and the trail is the distance between them.

That assumes the surface is the flat line our imaginary designer drew when he began detailing his suspension.

But now we're off-road. The front wheel is sinking into the surface. Aha. The contact patch moves forward, toward the steering axis line. Less trail. If there is no trail, the steering flops. There must be some trail, so off-road bikes begin with more than they'll use up.

Wow. I started this piece out by saying, “It all seems so simple.” By now, you'll agree, it’s anything but. I’ve showed rake and trail operating for/against you in at least four different modes, and probably haven’t exhausted all the possibilities. I've cited some good research that helps visualize motorcycle cornering response a little better, while suggesting how the big factories are beginning to hook a computer to the problem.

But at the level on which you and I operate, there are more variables than our two-dimensional minds can grasp at once. Lor us, it’s still easier and cheaper to build the bikes and fiddle with them by trialand-error.

That’s exactly what the moto-w’izards have done down through the years. As “everybody knows”—you. me. and the voodoo master who builds Morinis. ES