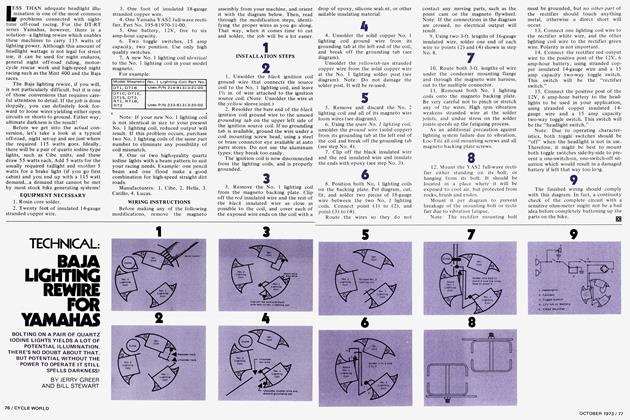
TECHNICAL: FLYWHEELS
Universally Accepted Myths Make Half Of What You Know Wrong And The Other Half Half Wrong!
J. G. Krol
EVERY MOTORCYCLE must have a flywheel and the size of that component has tremendous impact on the machine's overall riding qualities, yet this seemingly simple circle of steel is surrounded by scores of nonsensical myths. Half of what you hear about flywheels is wrong, and the other half is half wrong. The goal of this article is to cut through the myths and to give you a basic understanding of what flywheels are, what they do, and how they do it.
MECHANICAL CONSIDERATIONS
Physically, a flywheel is one of the more-or-less disc-shaped chunks of metal found on a crankshaft; but then, a gas tank cap is also a disc-shaped piece of metal, so this definition doesn't get to the heart of the matter. A flywheel is ultimately defined by what it does, and this is to resist angular acceleration by means of its inertia (full name: "moment of inertia").
The flywheel moves forward with the rest of the bike, and it also rotates. Its forward motion—like that of the frame, gas tank and rider—is governed by: Force = Mass x Acceleration. Mass is directly proportional to weight and acceleration is the rate of change of mph. The flywheel's rotational motion is governed by the analogous law: Torque = Inertia x Angular Acceleration, where angular acceleration can be thought of as the rate of change of rpm. Thus flywheel weight controls its forward motion and flywheel inertia controls its rotational motion.
Since power is just torque times rpm, it follows that a flywheel (1) absorbs power whenever it speeds up, (2) releases power whenever it slows down, and (3) neither absorbs nor releases power when it turns at any constant rpm.
Flywheels are often described as "heavy" or "light," which is unfortunate. An extra 10 lb. of flywheel weight does no more good than 10 lb. of lead ballast bolted to the frame. Flywheel weight is the price that has to be paid to gain the desired amounts of strength and inertia, and the less weight, the better. But some minimum amount of flywheel inertia is necessary for the engine to run at all. The problem is this: What is the relation between the mass (i.e., weight) and the inertia of a flywheel? The heavier flywheel is not necessarily the bigger flywheel, that is, more weight does not necessarily mean more inertia. It is entirely possible for a 10-lb. flywheel to have more inertia than a 20-lb. flywheel. Let's see how this can happen.
The inertia of a cylindrical flywheel is 1 = I/2MR2, where M is the mass and R is the radius (for irregular shapes one can calculate an equivalent "radius of gyration" to use in place of R). So a 10-lb. flywheel shaped like a phonograph record will have far more inertia than a 10-lb. flywheel shaped like a beer can, precisely because it has a much larger diameter.
To show the importance of shape and size even more clearly, we can do a bit of mathematical juggling to discover that the inertia of a cylindrical flywheel is proportional to dTR4, where d is the density of the material (steel is about three times as dense as aluminum) and T is the thickness of the disc. Doubling flywheel thickness doubles its inertia, but doubling the diameter multiplies inertia by a factor of sixteen since 24 = 2x2x2x2 = 16). Obviously inertia depends on mass, but it depends even more strongly on how that mass is deployed about the axis of rotation.
Each BB-sized particle of mass in a flywheel creates inertia proportional to the square of its distance from the centerline. A gram of mass near the rim produces very much more inertia than a gram of mass near the hub. Knowing this, designers often make flywheels thinner in the middle, thicker at the periphery. This gives more inertia with less weight. On the other hand, if you wanted to modify a flywheel to reduce its inertia as much as possible, machining a pound of weight off the rim would be more effective than removing a pound from near the center. Since a flywheel's main job is to provide inertia—and weight is only secondary—it is highly misleading to speak of "heavy" or "light” flywheels; it makes more sense to call them high-inertia or low-inertia flywheels...or simply, big and small flywheels. The inertia and weight of a flywheel are about as closely related as the throat diameter and weight of a carburetor: a heavier flywheel may or may not have more inertia, a heavier carburetor may or may not flow more air.
When the diameter of the crank discs is small relative to the diameter of the circle traced out by the crankpin (which is the stroke) and when the stroke is small relative to the displacement (an oversquare engine), you can expect the engine has rather little flywheel inertia for its size: Suzuki 400 MX, Honda 750, some Huskies. When crank disc diameter is much greater than stroke and when stroke is large compared to bore, you can expect the engine has rather much flywheel inertia for its size: Harley-Davidson V-Twins, old British Singles, ISDT Jawas. And a very large diameter external flywheel, as on a BMW or Moto-Guzzi, guarantees very high inertia. Because of the big difference between the effects of flywheel thickness and flywheel diameter in producing inertia, the eight crank discs of an oversquare four-cylinder engine normally provide more total weight but less total inertia than the two crank discs of an undersquare Single. This is fortunate since the Multi needs less inertia than the Single.
RIPPLE REDUCTION
The desired amount of flywheel inertia (including the crankshaft itself and everything hung on the ends of it, like an alternator or magneto or external flywheel) depends in a complicated way on many factors. The most important ones can be represented by the simplified formula, I = P/RfN2. Keeping this in mind to see how things tie together, let's take a look at the individual effects.
P is the peak-to-peak fluctuation in developed power. At the peak of the power stroke a cylinder may develop 150 bhp, while at the peak of the compression stroke it may produce -20 bhp—the minus sign indicating that power must flow into the engine to keep it going. Thus P = 170 brake horsepower. Yet the average brake horsepower, as measured on a dyno over a complete cycle of intake-compression-power-exhaust, may be only 30. During the power event the flywheel speeds up, absorbing the excess power; during the other events the flywheel slows down, sending power back to the engine.
Major effects: Fluctuation P is roughly proportional to the ordinary, average power (which we'll call bhp) of the engine. This suggests that bigger engines need bigger flywheels, as you'd expect, but it also points out that a flywheel big enough for full-throttle operation is more than big enough under partial-throttle conditions. P also depends strongly on the number of cylinders, since it measures the fluctuation in total power developed. Peaks and valleys in the instantaneous outputs of various cylinders from 1 to 2 drastically reduces P (relative to average power bhp, which we assume constant). Going from two to four cylinders reduces P significantly. Going from four to eight cylinders reduces P enough to notice. Going from eight to 16 cylinders reduces P by an imperceptible amount, as do further doublings to 32, 64, 128, and so on up to infinitely many cylinders. Thus the differences among one, two and four-cylinder motorcycle engines are much more noticeable than the difference between, say, a V-8 and V-12 automobile engine.
Minor effects: Higher compression ratio increases P at both ends of the scale...more power out at the peak of the power stroke and more power in at the peak of the compression stroke. P is somewhat bigger, hence a somewhat larger flywheel is indicated, when firing intervals are irregularly spaced, as in a V-Twin or a parallel Twin with a 180-degree crank.
R is the percent ripple in rpm: the difference between maximum instantaneous rpm (near the end of the power stroke) and minimum instantaneous rpm (near the end of the compression stroke), expressed as a percentage of the average rpm (as measured by an ordinary tachometer). R must be kept below some tolerable level to provide smooth running and a smooth flow of power through the chains, gears, shafts and splines of the power train. Many efforts to couple two engines together have come to grief over this. Phasing the engines so one crank is speeding up while the other is slowing down effectively doubles the ripple seen by the coupling chains or gears, often destroying them in short order. Powertrain components just plain don't like high frequency, back-andforth fluctuations in load. One solution is to phase the two engines to fire together; another is to add hefty supplementary flywheels to each crankshaft which, per above formula, cuts the ripple to tolerable levels. In principle, a designer can make the ripple as small as he wants by choosing high enough flywheel inertia.
Frequency f is the frequency of power impulses (we're ignoring the very complicated matter of the actual shape of the instantaneous power curve). Since a two-stroke fires every turn of the crank, it has f = N (N being the rpm); a four-stroke has f = 1/2N. According to the formula, therefore, a two-stroke needs less flywheel inertia than a four-stroke, everything else being equal. Furthermore, if there are C cylinders, f becomes CN for two-strokes and 1/2CN for four-strokes. Notice that increasing the number of cylinders has a powerful effect because it does two things: reduces P and increases f, both things indicating that less inertia is needed when the engine has more cylinders.
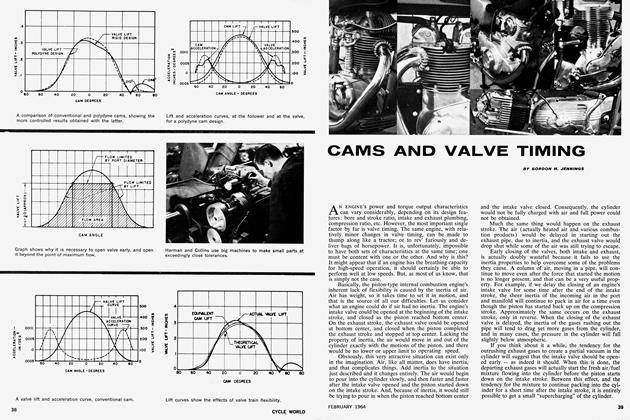
Having compared different kinds of engines, let's look at what happens in one given engine when rpm changes. Ripple will be given by R = P/lfN2. Now P will be proportional to average power bhp (itself a function of rpm) for a given engine; I, of course, will be fixed; f will be proportional to rpm; and N is rpm itself. So the percent ripple as a function of rpm will have the form: R = bhp/N3. As you know, bhp rises to a peak at some value of N (N = 7000 in the illustration). bhp/N (which is proportional to torque) must reach its peak at a lower rpm (N = 4500 in the illustration); bhp/N3 must peak at yet a lower speed (N = 3000 in the illustration); and bhp/N3 (which is percent ripple) must peak at an even lower rpm (N = 2500 in the illustration). Both in theory and in practice, the ripple will be greatest—the engine will run the roughest—at or very near the lowest rpm at which it is willing to hold steady under full throttle load. This is purely a flywheel effect and has nothing to do with carburetion, ignition, valve timing, or any of the other tuning parameters about which so much fuss is made!
Given a big enough flywheel even the wildest racing engine will lug down to very low rpm on a dyno. It may develop ridiculously little power, it may overheat, it may guzzle inordinate amounts of fuel, it may pound out its bearings, but it will run. And while it runs, it will deliver power smoothly, provided only that the flywheel is big enough. On the other hand, a mildly timed, small-carb, low compression ratio engine will refuse to run at low rpm if it has too small a flywheel.
The designer will pick flywheel inertia in accord with the factor P/RfN3 which, as we've just seen, varies widely with engine configuration and operating speed. Because there is a practical upper limit on the inertia (chiefly a limit on the diameter of the crank discs that will fit under the pistons) it often happens that engines with very large values of P/fN3 have high flywheel inertia and high residual ripple. Similarly, there is a practical lower limit on inertia (since something has to be there to connect the main bearings to the crankpins), so engines with very small values of P/fN3 often have low flywheel inertia and low residual ripple. For example, a low-speed, single-cylinder, four-stroke motorcycle engine responds slowly to throttle-blipping (a sign of high inertia), yet has so much ripple in its output that the rider can sometimes feel individual power pulses. At the other extreme, a V-12 responds eagerly to the throttle (low inertia), yet its power delivery is exceptionally smooth and even (low ripple).
Since ripple automatically decreases as rpm goes up, an engine designed for high speed operation can get by with a much smaller flywheel than a similar engine intended for low speed use. A 250cc motocross engine is ported to provide more power at high rpm than a similar 250cc enduro engine—though the latter probably has the edge in power at lower rpm. Naturally, the designer assumes that each engine will spend most of its time running in the rpm range where its output is most favorable, so he'll provide a small flywheel for the motocross bike and a big flywheel for the enduro bike. This is what he will normally do, but there is absolutely no reason why he has to. He could put a smaller flywheel on the enduro bike, in which case it would not be happy about running at slow speeds. He could put a big flywheel on the motocross bike, in which case its low speed running would be much improved.
Perhaps the best example of this arises between two-strokes and four-strokes. In principle, a two-stroke needs less inertia because its power pulses come at twice the frequency of a four-stroke's. For many years, therefore, two-strokes did in fact come with smaller flywheels than equal displacement four-strokes. And for many years motorcyclists nodded their heads wisely and intoned, "Two-strokes have no low-end pulling power, no low-end torque." Today, the motorcycles which have the most outstanding low speed performance of anything on the market—namely, trials bikes—are all twostrokes! These trials bikes have very large flywheels, of course, and that is the real explanation behind their performance.
The Single vs. Twin vs. Multi argument is another example of the same thing. The designer can get by with less inertia on a Multi than on a Single, so he usually does just that. Feeling the obvious seat-of-the-pants effects of flywheel inertia, riders jump to the conclusion that the number of cylinders, in itself, causes the observed differences. Not so. Mount a big enough flywheel on a Multi and it will feel completely different; it will seem to have far more "low end torque."
RIDING QUALITIES
How does flywheel inertia—regardless of how or why it was provided by the engine designer—influence the overall riding qualities of a motorcycle? Let's look at several of the main effects.
Suppose that the rear wheel, under power, hits a patch of poor traction: sand, oil, mud, etc. The wheel breaks loose and starts to spin faster than appropriate to the forward speed of the bike. In this situation, the faster the wheel spins, the less forward thrust it actually develops, hence the less thrust is available to propel the machine forward and the greater the likelihood that the wheel will trench down into the ground. The bigger the flywheel, the slower it will accelerate for a given amount of power developed by the engine. Thus at each instant after the tire starts to slip it will be slipping less and developing more forward thrust. Since undersquare, singlecylinder four-strokes usually come with much more flywheel inertia than oversquare, multi-cylinder two-strokes, the former kind of bike has developed a well-deserved reputation for traction-finding ability that can pull you clean through terrain-badness you never expected to survive. But if the latter kind of bike were equipped with equally large flywheels it would behave quite the same way! The traction-finding ability, or lack of it, is directly due to the flywheel, not to the configuration of the engine.
Big flywheels smooth and regulate the engagement of the tire with the ground and the engagement of the clutch as well. A bike with small flywheels will be "jerky" and "stally" off the line; any error in synchronizing throttle and clutch will result in an abrupt stall. Big flywheels allow you to be much more casual; feeding the clutch a bit too fast may cause the engine to bog down; but it will pull back up without stalling. Quick, clean, almost instant stalls, however induced, are a sign of small flywheels; slow, labored, grind-down-tc a-stop stalls indicate big flywheels.
Starting off in mud, a deep sandwash, or from the very foot of a steep hill with no running start possible combines the problems of clutch engagement and tire engagement. A small flywheel bike may be able to climb a certain hill easily, given a running start, but will be helpless against the same hill from a standing start at the bottom—or part way up. A big flywheel bike can climb without a running start just about anything that it can climb with a running start.
Cornering near the limit of tire adhesion is inherently easier with a bigger flywheel, for the lateral forces developed by a tire drop off much like the axial forces once the tire starts to spin. J.A.P. and ESO speedway bikes have plenty of flywheel inertia in order to be controllable in the corners. The big flywheels of a Harley add to its controllability on a flat track and, to give a counterexample, when the Yamaha 650 Twin was first adapted to flat-tracking, some tuners found it advisable to add flywheel inertia to the machine in order to improve its controllability. Since motocross bikes usually corner by bouncing off of berms, they do not need as much flywheel inertia.
The greater the flywheel inertia, the slower the engine can be made to idle reliably and the slower the motorcycle can be ridden in top gear without incurring "chain snatch," the extreme form of very high ripple that will literally destroy the powertrain if continued for any length of time. This effect depends on the amount of inertia compared to the "desired" amount described by P/fl\|2, but the previous effects depend on the amount of flywheel inertia regardless of the engine configuration. A 12,000 rpm oversquare V-12 two-stroke could be provided with flywheels that looked like they came off something made by Baldwin-Lima-Hamilton...in which case its traction-finding and general controllability would be just like any other bike with equally large flywheels. Under transient conditions the behavior of a motorcycle—its feel and responsiveness and controllability—is chiefly determined by the inertia of its flywheels, not by the length of its stroke, not by the number of its cylinders, not by the timing of its ports or valves, not by its gearing, not by the tread pattern of its tires, not—in other words—by all those factors that everybody chatters about constantly...while ignoring the flywheel.
So far it might seem that more flywheel inertia is always better than less, but there is another side to the story. Shifting is slower and trickier with big flywheels because you have to be more careful about synchronizing engine and transmission speeds during upshifts and, especially, downshifts—and it takes longer to achieve this. Force an unsynchronized downshift during the panic stop of a big flywheel motorcycle and you are likely to lock up the rear tire momentarily, provoking a slide. This is purely a flywheel effect and is not due to "compression braking" as is so commonly claimed. If it were due to compression braking, you could slide the rear tire merely by closing the throttle abruptly. What's really happening is that the downshift commands the flywheel instantly to jump to a higher rpm, which the flywheel refuses to do "instantly" since, after all, its whole purpose for being there is to resist sudden changes in rpm. Part (not all) of the low compression braking of a two-stroke, compared to a four-stroke, is due to the smaller flywheel usually found on a two-stroke.
The most important limitation on flywheel inertia comes from its impact on acceleration. The available, limited engine power has to provide forward acceleration to all the mass of the system (a small part of which is flywheel mass) at the same time that it is providing angular acceleration to all the inertia of the system (most of which is flywheel inertia). Obviously, the more the flywheel inertia, the more power is swallowed up in accelerating it and the less is available for the desired forward acceleration. Not so obviously, the amount of power required to accelerate a given flywheel at a given rate increases in proportion to the angular speed of the flywheel. If 1 bhp provides an acceleration of 1 rpm per second at 1000 rpm, it takes 2 bhp to provide this same acceleration at 2000 rpm. After some mathematical juggling, it turns out that the amount of power going to angular acceleration of the flywheel varies as the square of the overall gear ratio. If the overall spread of the gearbox, between low and top gear, is 3.1:1 (a moderately wide-ratio box), the square of this spread will be 10:1, meaning that flywheel acceleration swallows ten times as much power in low gear as it does in top gear.
In top gear, the power required to accelerate the flywheel is typically only 5 percent to 10 percent of the power used to provide forward acceleration of the motorcycle. In low gear, this jumps to 50 percent to 100 percent. That is, out of a total 25 bhp available, 10 bhp will accelerate the mass of the bike, 10 bhp will angularly accelerate the inertia of the flywheel, and 5 bhp will accelerate the mass of the rider (assuming he weighes half as much as the bike). If the designer assumes that his customers want blinding, neck-snapping acceleration in the lower gears—as he often does assume—he has a very strong motivation for providing the smallest amount of flywheel inertia he reckons he can get away with. This is the main reason why engines than can tolerate lower inertia (due to a small value of P/fN2) almost always have lower inertia. This is the main reason why most motorcycle engines have the least inertia the designer dares to provide. This is the main reason why some motorcycles definitely err on the side of too little inertia, e.g., the notorious Suzuki 400 MX for which accessory firms are actually selling extra bolt-on flywheels to "tame" it, as they say, and to make it more controllable. Most of all, the designer's motivation to get by with minimum flywheel inertia is the main reason why slow-revving, long-stroke, single-cylinder four-strokes conventionally have far more flywheel inertia than high-speed, oversquare, multi-cylinder twostrokes—and this, in turn, is why so many riders are misled into thinking that the engine configuration in itself is responsible for the obvious differences in riding qualities.
Big flywheels make a machine forgiving and easy to ride. They emphasize smoothness, traction-finding ability, good manners at low rpm, ease of manipulating clutch and throttle, in short, controllability.
Small flywheels make a machine quick and responsive, but demand greater skill and attention from the rider. They emphasize blinding acceleration, especially in the lower gears, and a generally racer type of performance.
Under easygoing conditions flywheel inertia makes little difference. Cruising down a straight and level road at 40 mph you'd be hard put to tell whether a bike has very big or very small flywheels. The more demanding the riding conditions become, however, the more important it is to proportion flywheel inertia to the terrain, the skill of the rider, the power/weight ratio of the bike, and so on. There is, therefore, no single answer for optimum flywheel inertia, but there is a simple, inclusive rule-of-thumb that you can use to determine whether you, with your skills, your riding conditions, your reflexes, your type of terrain, need more or less flywheel inertia:
You need more flywheel inertia if you are constantly having trouble controlling the power: if you are constantly stalling, getting hung up in a rear tire trench, fighting the coordination of clutch and throttle, struggling to get through difficult obstacles, sliding out on corners, getting stuck in the mud or sand, etc. If you rarely have such difficulties, you could use less flywheel inertia.
CONCLUSION
In summary, we see that there are three distinct sets of factors which bear on flywheel inertia.
First, since flywheel inertia is predominantly dependent on flywheel diameter, it is mechanically convenient to provide more inertia whenever a larger diameter can be accommodated. Thus, higher inertia goes with larger stroke/bore ratios, fewer cylinders, shorter piston skirts, and larger con-rodlength/stroke ratios.
Second, since the flywheel must be big enough to smooth the percentage rpm ripple to levels that will not damage the powertrain components, smooth running demands different amounts of inertia for different engine configurations and operating conditions. Thus, higher inertia goes with fewer cylinders, more "strokes" in the operating cycle (i.e., fourstroke vs. two-stroke), lower normal operating rpm, higher compression ratios, and less even firing intervals among cylinders.
Third, since the amount of flywheel inertia strongly influences the transient behavior of the entire motorcycle, good riding qualities require the inertia to be matched to the rider and to the riding conditions.
It's fair to say that these three considerations are listed in order of decreasing interest to the engine designer, but in order of increasing interest to the rider. Furthermore, there's no general reason why all three indicators of inertia must point in the same direction. It was not mechanically convenient, for example, for Bultaco to gain the additional inertia needed to convert the El Bandito racer into the El Montadero enduro bike: the crankcases on this short-stroke engine simply weren't big enough to accommodate a flywheel of the desired diameter. Bultaco was forced to use an extremely thick, yet small diameter, external flywheel that encumbers the bike with as much as 10 lb. of extra weight. The thing to do in
considering any motorcycle, therefore, is to examine it from each of these three viewpoints before reaching any conclusions about its flywheel inertia: mechanical convenience, smooth running, riding qualities.
That riders, even knowledgeable competitors, do not often do this was demonstrated by the covey of Kawasaki Mach Ills which showed up at a recent Southern California h il Ici ¡mb. Everything we've been saying about flywheel inertia in terms of stroke, number of cylinders, operating rpm, low-gear acceleration and so on leads us to expect the Mach III to have very low inertia which, when translated into riding qualities, predicts a machine that will spend half its time stalling and bogging-down, the other half of its time looping and trenching-in. That is exactly what this pack of Kwackers did, until they were eliminated, whence they slunk away dragging their "torque pipe" expansion chambers behind them. When somebody finally figures out that what these bikes need to be successful slope-shooters is much, much more flywheel inertia—and not further futile fiddling with carburetion, port timing and the like—and when he finds a practical way to graft it on...watch out!
Flywheel inertia interacts with but is not the same thing as flywheel weight, engine configuration, engine and chassis tuning parameters, operating conditions and riding qualities. Failure to realize this has created scores of myths that aren't so much wrong as they are simply misdirected. An estimated 813,967 road tests have tried to explain the observed riding qualities of a test bike in terms of its carburetion, gearing, tires, engine configuration, etc., when the real explanation was to be found in its flywheel inertia. The same thing often happens when owners are modifying their bikes: they forget that flywheel inertia is an important independent variable that must be coordinated with the other design variables for best results—just as carb size and valve size are independent variables that must be coordinated with each other for balanced performance. If you want a bike with the legendary "gobs of low-end torque," concentrate on those machines with plenty of flywheel inertia; and if you want acceleration that will squash your eyeballs in their sockets, concentrate on machines with minimal flywheel inertia.